Kuo vyresni mokiniai, tuo greičiau reikia sprendžiant paprastas problemas. Egzaminuose neskiriama daug laiko paprastiems pavyzdžiams ar problemoms ilgai spręsti. Kaip greitai ir lengvai rasti kvadrato įstrižainę? To vaikai mokomi nuo aštuntos klasės. Šiame straipsnyje pateikiami du būdai - vienas ilgesnis, kitas greitesnis.
Kaip apskaičiuoti kvadrato įstrižainę?
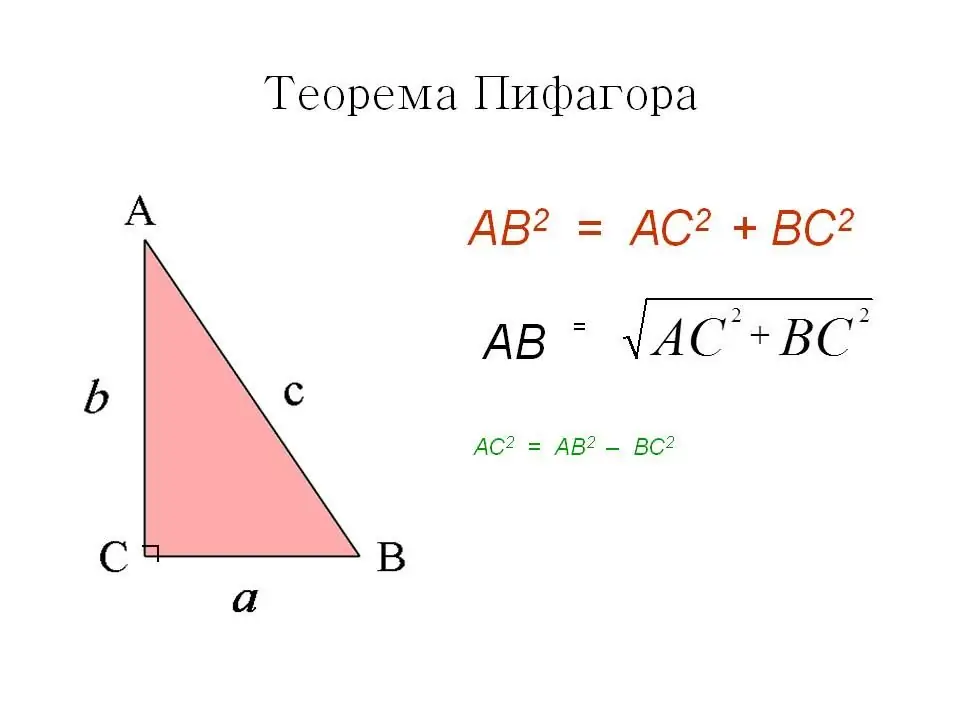
Pirmasis būdas yra gerai žinoma ir pažįstama Pitagoro teorema. Kvadrate visi kampai yra statūs, o tai reiškia, kad įstrižainė padalija jį į du lygius stačiakampius trikampius ir pati yra jų hipotenuzė. Pagal Pitagoro teoremą hipotenuzės kvadratas yra lygus kojų kvadratų sumai.

Antras būdas yra paprasta formulė, kuri būdinga tik kvadratams, ir jums tereikia ją atsiminti. Kaip žinote, visos kvadrato kraštinės yra lygios, todėl matematikai apskaičiavo tokią jo įstrižainės formulę: ji lygi kraštinės ir dviejų šaknies sandaugai.
Žinoma, geriausia tiesiog atsiminti kvadrato įstrižainės ilgio formulę ir ją naudoti visada, nes taip daug greičiau ir patogiau. Tai ypač jaučiama sprendžiant uždavinius tiesiogine forma, kur vietoj didelių šaknų išraiškų galite apsieiti su vienu produktu.
Pavyzdys
Paimkite, pavyzdžiui, kvadratą 6 x 6, tai yra, kurio kraštinė lygi šešiems centimetrams.
Pagal pirmąjį metodą: tegul įstrižainė yra C, o kraštinė A.
Tada gauname, kad C=√A^2+A^2 arba C=√2A^2.
Parašykime skaitine forma: С=√36 + 36. Gavome √72, tai yra 3√8 arba 6√2.
O dabar suraskime tą pačią įstrižainę, bet antruoju metodu: C=A√2 arba skaitine forma: 6√2
Dabar matote, kiek antrasis metodas yra greitesnis, lengvesnis ir, svarbiausia - efektyvesnis, ypač sprendžiant tokius lengvus uždavinius, nes egzamine brangi kiekviena minutė!
Kitos kvadratinių įstrižainių savybės
Be to, kad žinote, kaip rasti kvadrato įstrižaines, turite žinoti ir jų savybes. Pagrindiniai yra:
- Įstrižainės yra lygios viena kitai, o susikirtimo taškas padalintas per pusę.
- Jie sudaro stačius kampus, kai susikerta.
- Padalinkite kvadratą į vienodus trikampius.
Išvada
Klausimą, kaip suskaičiuoti kvadrato įstrižaines, dažniausiai užduoda mokiniai, kurie mokykloje šios temos praleido. Tačiau tokias pagrindines matematikos taisykles turėtų žinoti kiekvienas! Pageidautina išspręsti kuo greičiau, o tam reikia žinoti sutrumpintas formules. Visa tai labai paprasta ir lengva, betkartu tai yra pagrindas, būtinas sprendžiant daug sudėtingesnes problemas ateityje. Svarbi šio pagrindo dalis yra aikštė.






