Tipiniai apšvietimo efektai, su kuriais kiekvienas žmogus dažnai susiduria kasdieniame gyvenime, yra atspindys ir lūžis. Šiame straipsnyje mes nagrinėsime atvejį, kai abu efektai pasireiškia tame pačiame procese, kalbėsime apie vidinio totalinio atspindžio reiškinį.
Šviesos atspindys
Prieš nagrinėdami vidinio visiško šviesos atspindžio reiškinį, turėtumėte susipažinti su įprasto atspindžio ir lūžio poveikiu. Pradėkime nuo pirmojo. Paprastumo dėlei svarstysime tik šviesą, nors šie reiškiniai būdingi bet kokio pobūdžio bangai.
Atspindys suprantamas kaip vienos tiesios trajektorijos, kuria juda šviesos spindulys, pasikeitimas į kitą tiesiąją trajektoriją, kai jis savo kelyje susiduria su kliūtimi. Šį efektą galima pastebėti nukreipus lazerinį žymeklį į veidrodį. Dangaus ir medžių vaizdų atsiradimas žiūrint į vandens paviršių taip pat yra saulės šviesos atspindžio rezultatas.

Atspindžiui galioja šis dėsnis: kampaikritimas ir atspindys yra toje pačioje plokštumoje kartu su statmena atspindinčiam paviršiui ir yra lygūs vienas kitam.
Šviesos lūžimas
Lūžio poveikis panašus į atspindį, tik jis atsiranda, jei kliūtis šviesos pluošto kelyje yra kita skaidri terpė. Šiuo atveju dalis pradinio pluošto atsispindi nuo paviršiaus, o dalis pereina į antrąją terpę. Ši paskutinė dalis vadinama lūžusiu pluoštu, o kampas, kurį ji sudaro statmenai sąsajai, vadinamas lūžio kampu. Lūžęs spindulys yra toje pačioje plokštumoje kaip ir atsispindėjęs bei krintantis spindulys.
Stiprūs lūžio pavyzdžiai yra pieštuko lūžimas vandens stiklinėje arba apgaulingas ežero gylis, kai žmogus žiūri žemyn į jo dugną.

Matematiškai šis reiškinys aprašomas naudojant Snello dėsnį. Atitinkama formulė atrodo taip:
1 sin (θ1)=n2 nuodėmė (θ 2).
Čia kritimo ir lūžio kampai atitinkamai pažymėti kaip θ1 ir θ2. Dydžiai n1, n2 atspindi šviesos greitį kiekvienoje terpėje. Jie vadinami terpės lūžio rodikliais. Kuo didesnis n, tuo lėčiau šviesa sklinda tam tikra medžiaga. Pavyzdžiui, vandenyje šviesos greitis yra 25% mažesnis nei ore, todėl jo lūžio rodiklis yra 1,33 (oro jis yra 1).
Visiško vidinio atspindžio reiškinys
Šviesos lūžio dėsnis veda prie vienoįdomus rezultatas, kai spindulys sklinda iš terpės su dideliu n. Leiskite mums išsamiau apsvarstyti, kas šiuo atveju atsitiks su sija. Išrašykime Snello formulę:
1 sin (θ1)=n2 nuodėmė (θ 2).
Manysime, kad n1>n2. Šiuo atveju, kad lygybė išliktų teisinga, θ1 turi būti mažesnė nei θ2. Ši išvada galioja visada, nes atsižvelgiama tik į kampus nuo 0o iki 90o, kurių ribose sinuso funkcija nuolat didėja. Taigi, paliekant tankesnę optinę terpę ne tokiai tankiai (n1>n2), spindulys labiau nukrypsta nuo įprasto.
Dabar padidinkime kampą θ1. Dėl to ateis momentas, kai θ2 bus lygus 90o. Įvyksta nuostabus reiškinys: iš tankesnės terpės skleidžiamas spindulys liks jame, tai yra, jam sąsaja tarp dviejų skaidrių medžiagų taps nepermatoma.
Kritinis kampas
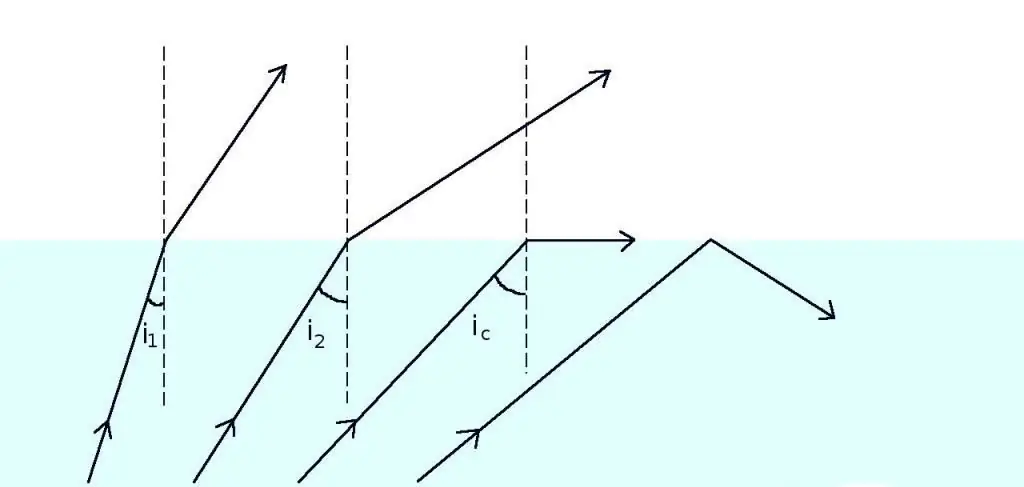
Kampas θ1, kuriam θ2=90o, vadinamas kritinė nagrinėjamai žiniasklaidos porai. Bet koks spindulys, patekęs į sąsają kampu, didesniu už kritinį kampą, visiškai atsispindi pirmoje terpėje. Kritiniam kampui θc galima parašyti išraišką, kuri tiesiogiai išplaukia iš Snell formulės:
sin (θc)=n2 / n1.
Jeiantroji terpė yra oras, tada ši lygybė supaprastinama iki formos:
sin (θc)=1 / n1.
Pavyzdžiui, kritinis vandens kampas yra:
θc=arcsin (1/1, 33)=48, 75o.
Jei pasinersite į baseino dugną ir pažvelgsite į viršų, dangų ir per jį bėgančius debesis matysite tik virš savo galvos, likusioje vandens paviršiaus dalyje bus matomos tik baseino sienos.
Iš aukščiau pateiktų samprotavimų aišku, kad, skirtingai nei refrakcija, visiškas atspindys nėra grįžtamasis reiškinys, jis atsiranda tik pereinant iš tankesnės terpės į mažiau tankią, bet ne atvirkščiai.
Visiškas atspindys gamtoje ir technologijose
Turbūt labiausiai paplitęs efektas gamtoje, kuris neįmanomas be visiško atspindžio, yra vaivorykštė. Vaivorykštės spalvos yra b altos šviesos sklaidos lietaus lašuose rezultatas. Tačiau kai spinduliai patenka į šių lašelių vidų, jie patiria vieną arba dvigubą vidinį atspindį. Štai kodėl vaivorykštė visada atrodo dviguba.
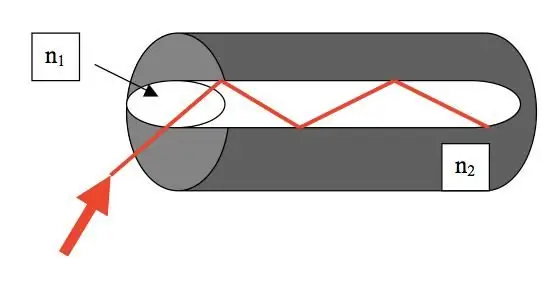
Vidinio visiško atspindžio reiškinys naudojamas šviesolaidinėje technologijoje. Dėl optinių skaidulų galima be nuostolių perduoti elektromagnetines bangas dideliais atstumais.






