Ticijaus-Bodo taisyklė (kartais tiesiog vadinama Bodo dėsniu) yra hipotezė, kad kūnai kai kuriose orbitinėse sistemose, įskaitant Saulę, sukasi išilgai pusiau ašių, priklausomai nuo planetų sekos. Formulė rodo, kad kiekviena planeta, besitęsianti į išorę, bus maždaug dvigubai toliau nuo Saulės nei ankstesnė.
Ši hipotezė teisingai numatė Cereros (asteroido juostoje) ir Urano orbitas, tačiau nepavyko nustatyti Neptūno orbitos ir galiausiai ją pakeitė Saulės sistemos formavimosi teorija. Jis pavadintas Johano Danielio Titiuso ir Johano Elerto Bode vardu.

Origins
Pirmą kartą paminėta serija, artima Bodės dėsniui, yra David Gregory knygoje „Astronomijos elementai“, išleistoje 1715 m. Jame jis sako: „… darant prielaidą, kad atstumas nuo Saulės iki Žemės yra padalintas į dešimt lygių dalių, iš kurių Merkurijaus atstumas bus maždaug keturios, nuo Veneros - septyni, nuo Marso - penkiolika, nuo Jupiterio - penkiasdešimt du., o iš Saturno devyniasdešimt penkiPanašus pasiūlymas, tikriausiai įkvėptas Gregorio, pateikiamas Christiano Wolffo 1724 m. išleistame darbe.
1764 m. Charlesas Bonnet savo knygoje „Gamtos apmąstymas“sakė: „Mes žinome septyniolika planetų, sudarančių mūsų saulės sistemą [tai yra pagrindinės planetos ir jų palydovai], bet nesame tikri, kad jų nebėra“. Prie to 1766 m. savo Bonnet kūrinio vertime Johanas Danielis Titiusas pridėjo dvi savo pastraipas 7 puslapio apačioje ir 8 puslapio viršuje. Naujos interpoliuotos pastraipos originaliame Bonnet tekste nėra: nei italų kalba. nei kūrinio vertimų į anglų kalbą.
Ticijaus atradimas
Įterptame Ticijaus tekste yra dvi dalys. Pirmasis paaiškina planetų atstumų nuo Saulės seką. Jame taip pat yra keli žodžiai apie atstumą nuo Saulės iki Jupiterio. Bet tai dar ne teksto pabaiga.
Verta pasakyti keletą žodžių apie Titius-Bode taisyklės formulę. Atkreipkite dėmesį į atstumus tarp planetų ir išsiaiškinkite, kad beveik visos jos yra atskirtos viena nuo kitos proporcija, atitinkančia jų kūno dydžius. Padalinkite atstumą nuo Saulės iki Saturno iš 100 dalių; tada Merkurijų nuo Saulės skiria keturios tokios dalys; Venera - į 4 + 3=7 tokias dalis; Žemė - pagal 4+6=10; Marsas - 4+12=16.
Tačiau atkreipkite dėmesį, kad nuo Marso iki Jupiterio yra nukrypimų nuo šios tokios tikslios eigos. Iš Marso seka 4+24=28 tokių dalių erdvė, tačiau iki šiol ten nebuvo aptikta nė vienos planetos. Bet ar lordas Architektas turėtų palikti šią vietą tuščią? Niekada. TaigiDarykime prielaidą, kad ši erdvė, be jokios abejonės, priklauso dar neatrastiems Marso palydovams, ir pridurkime, kad galbūt Jupiteris aplinkui dar turi kelis mažesnius palydovus, kurių dar nematė joks teleskopas.

Bodos kilimas
1772 m. Johanas Elertas Bode, būdamas dvidešimt penkerių metų, baigė antrąjį savo astronominio sąvado Anleitung zur Kenntniss des gestirnten Himmels („Žvaigždėtojo dangaus pažinimo vadovas“) leidimą. pridėjo šią išnašą, kuri iš pradžių nebuvo š altinio, bet pažymėta vėlesnėse versijose. Bodės atsiminimuose galima rasti nuorodą į Titijų, aiškiai pripažįstant jo autoritetą.

Nuomonių pareiškimas
Taip skamba Titius-Bode taisyklė pateikiant pastarąjį: jei atstumas nuo Saulės iki Saturno imamas lygus 100, tai Merkurijų nuo Saulės skiria keturios tokios dalys. Venera - 4+3=7. Žemė - 4+6=10. Marsas - 4+12=16.
Dabar šioje tvarkingoje eigoje yra spraga. Po Marso seka erdvė su skaičiavimu 4+24=28, kurioje dar nematyta nė viena planeta. Ar galime patikėti, kad visatos įkūrėjas paliko šią erdvę tuščią? Žinoma ne. Iš čia pasiekiame Jupiterio atstumą skaičiavimo forma 4+48=52 ir galiausiai iki Saturno atstumo - 4+96=100.

Šie du teiginiai apie konkrečią tipologiją ir orbitos spindulius yra kilę iš senovėsastronomija. Daugelis šių teorijų atsirado dar iki XVII amžiaus.
Įtaka
Titis buvo vokiečių filosofo Christiano Freiherr von Wolff (1679-1754) mokinys. Antroji Bonnet kūrinio įterpto teksto dalis paremta 1723 m. von Wolffo darbu „Vernünftige Gedanken von den Wirkungen der Natur“.
XX amžiaus literatūra Titius-Bode taisyklės autorystę priskiria vokiečių filosofui. Jei taip, Ticijus galėtų iš jo pasimokyti. Kitą senesnę nuorodą parašė James Gregory 1702 m. savo Astronomiae Physicae et geometryae Elementa, kur planetų atstumų 4, 7, 10, 16, 52 ir 100 seka tapo geometrine santykio 2 progresija.
Tai artimiausia Niutono formulė. Ji taip pat buvo rasta Benjamino Martino ir Thomaso Ceardo raštuose prieš Bonnet knygos išleidimą Vokietijoje.
Tolimesnis darbas ir praktinės reikšmės
Ticijus ir Bodė tikėjosi, kad įstatymas leis atrasti naujas planetas, o Urano ir Cereros atradimas, kurių atstumas gerai sutampa su įstatymu, prisidėjo prie to, kad jį pripažintų mokslo pasaulis.
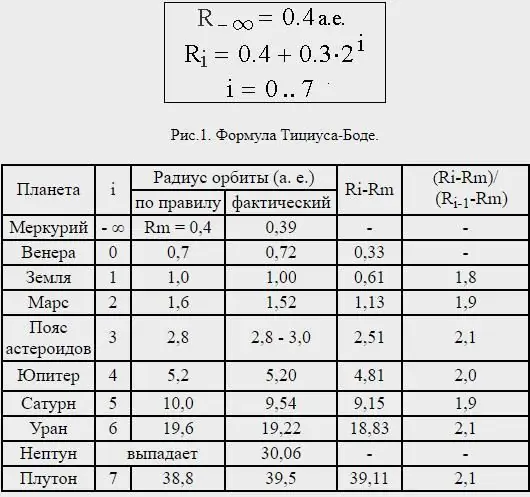
Tačiau Neptūno atstumas buvo labai nenuoseklus, ir iš tikrųjų Plutonas, kuris dabar nelaikomas planeta, yra vidutiniu atstumu, kuris maždaug atitinka Titius-Bode dėsnį, numatytą kitai planetai už Urano.
Iš pradžių paskelbtą dėsnį maždaug tenkino visos žinomos planetos - Merkurijus ir Saturnas - su atotrūkiu tarpketvirta ir penkta planetos. Tai buvo laikoma įdomia, bet ne itin svarbia figūra iki Urano atradimo 1781 m., kuris tinka serijai.
Remdamasis šiuo atradimu, Bode paragino ieškoti penktosios planetos. Cerera, didžiausias objektas asteroidų juostoje, buvo rastas numatytoje Bodės vietoje 1801 m. Bodės dėsnis buvo plačiai priimtas, kol 1846 m. buvo atrastas Neptūnas ir įrodyta, kad jis nesuderinamas su įstatymu.
Tuo pačiu metu daugybė juostoje aptiktų asteroidų išbraukė Cererą iš planetų sąrašo. Bodės dėsnį 1898 m. aptarė astronomas ir logikas Charlesas Sandersas Peirce'as kaip klaidingo samprotavimo pavyzdį.

Problemos raida
Plutono atradimas 1930 m. problemą dar labiau apsunkino. Nors tai ir neatitiko Bodės dėsnio numatytos pozicijos, tai buvo apie poziciją, kurią įstatymas numatė Neptūnui. Tačiau vėliau aptiktas Kuiperio diržas, ypač objektas Eris, kuris yra masyvesnis už Plutoną, bet neatitinka Bodės dėsnio, dar labiau diskreditavo formulę.
Serdos indėlis
Jėzuitas Thomas Cerda 1760 m. Barselonoje skaitė garsųjį astronomijos kursą Sant Jaume de Cordelle koledžo (Imperatoriškoji ir karališkoji Kordelio bajorų seminarija) Karališkojoje matematikos katedroje. Cerdaso „Tratado“rodomi planetų atstumai, gauti taikant trečiąjį Keplerio dėsnį, 10-3 tikslumu.
Jei laikysime 10 atstumą nuo Žemės irsuapvalinti iki sveikojo skaičiaus, geometrinė progresija [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, nuo n=2 iki n=8, gali būti išreikšta. Ir naudojant apskritą vienodą fiktyvų judesį į Keplerio anomaliją, Rn reikšmes, atitinkančias kiekvienos planetos santykius, galima gauti kaip rn=(Rn - R1) / (Rn-1 - R1), todėl gaunamas 1,82; 1, 84; 1, 86; 1,88 ir 1,90, kur rn=2 - 0,02 (12 - n) yra aiškus ryšys tarp Keplerio tęstinumo ir Titius-Bode dėsnio, kuris laikomas atsitiktiniu skaitiniu sutapimu. Skaičiavimo rezultatas yra artimas dviem, bet dvivietis gali būti laikomas skaičiaus 1, 82 apvalinimu.

Vidutinis planetos greitis nuo n=1 iki n=8 sumažina atstumą nuo Saulės ir skiriasi nuo vienodo mažėjimo, kai n=2, kad atsigautų nuo n=7 (orbitos rezonansas). Tai turi įtakos atstumui nuo Saulės iki Jupiterio. Tačiau atstumas tarp visų kitų objektų, laikantis liūdnai pagarsėjusios taisyklės, kuriai skirtas straipsnis, taip pat priklauso nuo šios matematinės dinamikos.
Teorinis aspektas
Nėra tvirto teorinio paaiškinimo, pagrindžiančio Titius-Bode taisyklę, tačiau gali būti, kad atsižvelgiant į orbitos rezonanso ir laisvės laipsnių trūkumo derinį, bet kuri stabili planetų sistema turi didelę tikimybę pakartoti aprašytą modelį. ši dviejų mokslininkų teorija.
Kadangi tai gali būti matematinis sutapimas, o ne „gamtos dėsnis“, kartais tai vadinama taisykle, o ne „dėsniu“. Tačiau astrofizikas Alanas Bossas teigia, kad taip yra paprasčiausiaisutapimas, o planetos mokslo žurnalas „Icarus“nebepriima straipsnių, kuriuose bandoma pateikti patobulintas „įstatymo“versijas.
Orbitinis rezonansas
Orbitinis rezonansas iš pagrindinių orbitoje skriejančių kūnų sukuria aplink Saulę sritis, kuriose nėra ilgalaikių stabilių orbitų. Planetų formavimosi modeliavimo rezultatai patvirtina mintį, kad atsitiktinai parinkta stabili planetų sistema greičiausiai atitiks Titius-Bode taisyklę.

Dubrulle ir Graner
Dubrulle ir Graner parodė, kad galios dėsnio atstumo taisyklės gali būti planetinių sistemų griūvančių debesų modelių, turinčių dvi simetrijas: sukimosi invariantą (debesis ir jo turinys yra ašies simetriški) ir mastelio invarianciją (debesis ir jo turinys visomis svarstyklėmis atrodo vienodas).
Pastaroji būdinga daugeliui reiškinių, kurie, kaip manoma, turi įtakos planetos formavimuisi, pavyzdžiui, turbulencijai. Atstumas nuo Saulės iki Saulės sistemos planetų, pasiūlytas Ticijaus ir Bodės, nebuvo peržiūrėtas atliekant Dubrulle ir Graner tyrimus.






