Fizikoje nagrinėjama lygiagretaus ir nuoseklaus ryšio tema, tai gali būti ne tik laidininkai, bet ir kondensatoriai. Čia svarbu nesusipainioti, kaip kiekvienas iš jų atrodo diagramoje. Ir tik tada taikyti konkrečias formules. Beje, reikia juos prisiminti mintinai.
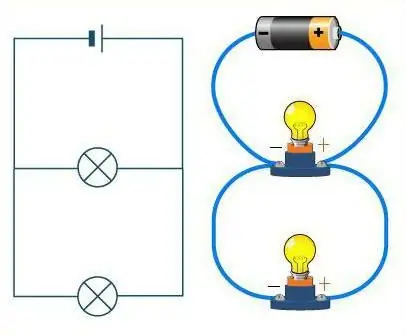
Kaip atskirti šiuos du junginius?
Atidžiai pažiūrėkite į diagramą. Jei laidai vaizduojami kaip kelias, tada jame esantys automobiliai atliks rezistorių vaidmenį. Tiesiu keliu be jokių išsišakų automobiliai važiuoja vienas po kito, grandine. Lygiai taip pat atrodo ir laidų nuoseklus sujungimas. Kelias šiuo atveju gali turėti neribotą posūkių skaičių, bet ne vienos sankryžos. Kad ir kaip vingiuotų kelias (laidai), mašinos (rezistoriai) visada bus viena po kitos, vienoje grandinėje.
Tai visai kas kita, jei atsižvelgiama į lygiagretų ryšį. Tada rezistorius galima palyginti su sportininkais pradžioje. Jie yrakiekvienas stovi savo takelyje, tačiau jų judėjimo kryptis ta pati, o finišo linija yra toje pačioje vietoje. Panašiai ir rezistoriai - kiekvienas iš jų turi savo laidą, bet visi jie tam tikru momentu yra sujungti.
Srovės stiprumo formulės
Tai visada aptarinėjama temoje „Elektra“. Lygiagrečios ir nuoseklios jungtys skirtingai veikia rezistorių srovės stiprumą. Jiems išvedamos formulės, kurias galima atsiminti. Tačiau užtenka tik prisiminti į juos įneštą prasmę.
Taigi, srovė nuosekliai sujungti laidininkus visada yra vienoda. Tai reiškia, kad kiekviename iš jų srovės stiprumo vertė nesiskiria. Galite padaryti analogiją, jei palyginsite laidą su vamzdžiu. Jame vanduo visada teka tuo pačiu keliu. Ir visos kliūtys jo kelyje bus nušluotos ta pačia jėga. Tas pats su srove. Todėl visos srovės formulė grandinėje su nuosekliu rezistorių prijungimu atrodo taip:
I gen=aš 1=aš 2
Čia raidė I reiškia srovės stiprumą. Tai įprastas žymėjimas, todėl turite jį atsiminti.
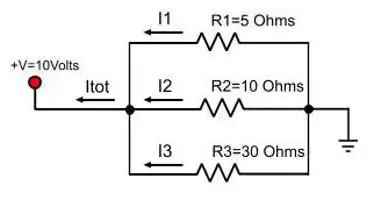
Srovė lygiagrečiame jungtyje nebebus pastovi vertė. Su ta pačia analogija su vamzdžiu paaiškėja, kad vanduo bus padalintas į du srautus, jei pagrindinis vamzdis turi šaką. Tas pats reiškinys pastebimas su srove, kai jos kelyje atsiranda laidų išsišakojimas. Suminio srovės stiprumo formulė, kai laidai prijungti lygiagrečiai:
I gen=aš 1 + aš 2
Jei šaka sudaryta iš laidų, kuriedaugiau nei du, tada aukščiau pateiktoje formulėje bus daugiau terminų tuo pačiu skaičiumi.
Streso formulės
Kai nagrinėjama grandinė, kurioje laidininkai yra sujungti nuosekliai, įtampa visoje sekcijoje nustatoma pagal šių reikšmių sumą kiekviename konkrečiame rezistorių. Šią situaciją galite palyginti su plokštelėmis. Vienam žmogui bus lengva vieną iš jų laikyti, antrąjį irgi galės paimti šalia, bet sunkiai. Vienas žmogus nebegalės trijų lėkščių vienas šalia kito laikyti, prireiks antros pagalbos. ir kt. Žmonių pastangos sumuojasi.
Grandinės atkarpos su nuosekliu laidų prijungimu įtampos formulė atrodo taip:
U gen=U 1 + U 2, kur U yra priimtas pavadinimas elektros įtampai.
Kita situacija susidaro, jei svarstomas lygiagretus rezistorių sujungimas. Kai lėkštės sukraunamos viena ant kitos, jas vis tiek gali laikyti vienas žmogus. Taigi jums nieko nereikia pridėti. Ta pati analogija pastebima, kai laidai yra sujungti lygiagrečiai. Kiekvieno iš jų įtampa yra vienoda ir lygi tai, kuri yra ant visų iš karto. Bendros įtampos formulė yra:
U gen=U 1=U 2
Elektrinės varžos formulės
Nebegalite jų įsiminti, bet žinote Omo dėsnio formulę ir iš jos išveskite norimą. Iš šio įstatymo išplaukia, kadįtampa lygi srovės ir varžos sandaugai. Tai yra, U=IR, kur R yra varža.
Tada formulė, su kuria turėsite dirbti, priklauso nuo to, kaip prijungti laidininkai:
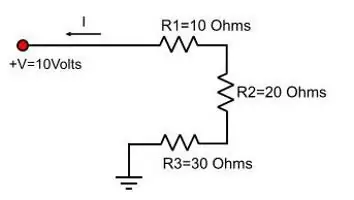
- serija, todėl reikia lygybės įtampai - IgenRiš viso=I1R1 + I2R2;
- lygiagrečiai, būtina naudoti srovės stiprumo formulę - Uviso / Riš viso=U 1/ R1 + U2 / R2 .
Sekė paprastos transformacijos, kurios pagrįstos tuo, kad pirmoje lygybėje visos srovės turi vienodą reikšmę, o antroje - įtampos yra lygios. Taigi juos galima sutrumpinti. Tai yra, gaunamos šios išraiškos:
- R gen=R 1 + R 2 (laidų nuosekliam prijungimui)
- 1 / R gen=1 / R 1 + 1 / R 2(kai prijungtas lygiagrečiai).
Kai prie tinklo prijungtų rezistorių skaičius didėja, terminų skaičius šiose išraiškose pasikeičia.
Verta pažymėti, kad lygiagretus ir nuoseklus laidininkų sujungimas turi skirtingą poveikį bendrai varžai. Pirmasis iš jų sumažina grandinės sekcijos varžą. Be to, pasirodo, kad jis yra mažesnis už mažiausią iš naudojamų rezistorių. Kai sujungiama nuosekliai, viskas yra logiška: reikšmės sumuojasi, todėl bendras skaičius visada bus didžiausias.
Darbo srovė
Ankstesni trys dydžiai sudaro lygiagrečio ryšio ir laidininkų nuoseklaus išdėstymo grandinėje dėsnius. Todėl juos žinoti būtina. Kalbant apie darbą ir galią, tereikia atsiminti pagrindinę formulę. Jis parašytas taip: A \u003d IUt, kur A yra srovės veikimas, t yra jos pratekėjimo per laidininką laikas.
Norėdami nustatyti bendrą darbą su nuosekliuoju ryšiu, turite pakeisti įtampą pradine išraiška. Gaunate lygybę: A \u003d I(U 1 + U 2)t, atidarydami skliaustus, kuriuose paaiškėja, kad visos sekcijos darbas yra lygus kiekvienam konkrečiam dabartiniam vartotojui.
Svarstymas vyksta panašiai, jei svarstoma lygiagretaus ryšio schema. Manoma, kad turi būti pakeista tik srovė. Bet rezultatas bus toks pat: A=A 1 + A 2.
Dabartinė galia
Išvedant grandinės sekcijos galios formulę (žymėjimas "P"), vėl reikia naudoti vieną formulę: P \u003d UI. Po tokių samprotavimų paaiškėja, kad lygiagrečios ir nuoseklios jungtys yra aprašyta tokia galios formule: P \u003d P1 + P 2.
Tai yra, kad ir kaip būtų sudarytos schemos, bendra galia bus darbe dalyvaujančių asmenų suma. Tai paaiškina faktą, kad vienu metu į buto tinklą neįmanoma įtraukti daug galingų įrenginių. Ji tiesiog negali atlaikyti krūvio.
Kaip laidų sujungimas įtakoja naujametinės girliandos remontą?
Iš karto perdegus vienai iš lempučių tampa aišku, kaip jos buvo sujungtos. Atnuoseklusis ryšys, nė vienas iš jų neužsidega. Taip yra dėl to, kad lempa, kuri tapo netinkama, sukuria grandinės pertrauką. Todėl turite viską patikrinti, kad nustatytumėte, kuris iš jų perdegė, pakeiskite jį - ir girlianda pradės veikti.
Jei jis naudoja lygiagrečią jungtį, jis nenustoja veikti, jei sugenda viena iš lempučių. Juk grandinė nenutrūks iki galo, o tik viena lygiagreti dalis. Norint taisyti tokią girliandą, nereikia tikrinti visų grandinės elementų, o tik tuos, kurie nešviečia.
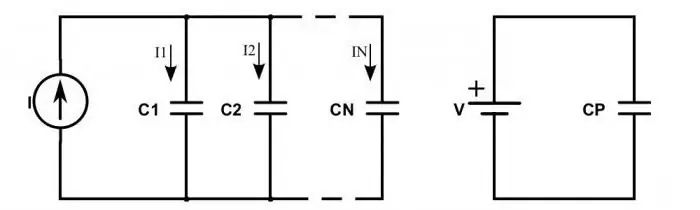
Kas atsitiks su grandine, jei vietoj rezistorių įtraukiami kondensatoriai?
Jus jungiant nuosekliai, stebima tokia situacija: įkrovimai iš maitinimo š altinio pliusų patenka tik į kraštutinių kondensatorių išorines plokštes. Tie, kurie yra tarp jų, tiesiog perduoda tą krūvį išilgai grandinės. Tai paaiškina faktą, kad ant visų plokštelių atsiranda tie patys krūviai, bet su skirtingais ženklais. Todėl kiekvieno nuosekliai sujungto kondensatoriaus elektros krūvį galima parašyti taip:
q gen =q 1=q 2.
Norėdami nustatyti kiekvieno kondensatoriaus įtampą, turėsite žinoti formulę: U=q / C. Joje C yra kondensatoriaus talpa.
Bendra įtampa atitinka tą patį dėsnį kaip ir rezistoriai. Todėl talpos formulėje įtampą pakeitę suma, gauname, kad bendra įrenginių talpa turi būti apskaičiuojama pagal formulę:
C=q / (U 1 + U2).
Galite supaprastinti šią formulę apversdami trupmenas ir pakeisdami įtampos ir įkrovimo santykį talpa. Pasirodo tokia lygybė: 1 / С=1 / С 1 + 1 / С 2.
Situacija atrodo kiek kitaip, kai kondensatoriai yra prijungti lygiagrečiai. Tada bendras krūvis nustatomas pagal visų įkrovų, susikaupusių ant visų prietaisų plokštelių, sumą. O įtampos vertė vis tiek nustatoma pagal bendruosius dėsnius. Todėl visos lygiagrečiai prijungtų kondensatorių talpos formulė yra tokia:
С=(q 1 + q 2) / U.
Tai reiškia, kad ši vertė laikoma kiekvieno jungtyje naudojamo įrenginio suma:
S=S 1 + S 2.
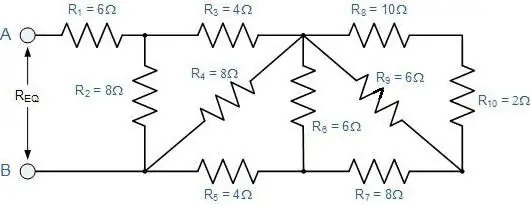
Kaip nustatyti bendrą savavališko laidininkų sujungimo varžą?
Tai yra tokia, kurioje nuoseklios sekcijos pakeičia lygiagrečias ir atvirkščiai. Jiems visi aprašyti dėsniai galioja iki šiol. Tik jums reikia juos taikyti etapais.
Pirma, tai turėtų mintyse išplėsti schemą. Jei sunku tai įsivaizduoti, tuomet reikia nupiešti, kas atsitiks. Paaiškinimas taps aiškesnis, jei panagrinėsime jį konkrečiu pavyzdžiu (žr. pav.).
Brėžti patogu pradėti nuo taškų B ir C. Jie turi būti išdėstyti tam tikru atstumu vienas nuo kito ir nuo lapo kraštų. Kairėje vienas laidas artėja prie taško B, o du jau nukreipti į dešinę. Kita vertus, taškas B turi dvi atšakas kairėje ir vieną laidą po jo.
Dabar turite užpildyti tarpą tarp jųtaškais. Išilgai viršutinės vielos turi būti dedami trys rezistoriai, kurių koeficientai yra 2, 3 ir 4, o iš apačios eis tas, kurio indeksas yra 5. Pirmieji trys yra sujungti nuosekliai. Su penktuoju rezistoriumi jie yra lygiagrečiai.
Likę du rezistoriai (pirmasis ir šeštasis) yra nuosekliai sujungti su nagrinėjama BV sekcija. Todėl piešinį galima tiesiog papildyti dviem stačiakampiais abiejose pasirinktų taškų pusėse. Belieka taikyti pasipriešinimo skaičiavimo formules:
- pirmiausia duotas nuosekliajam prijungimui;
- tada lygiagrečiai;
- ir dar kartą iš eilės.
Tokiu būdu galite įdiegti bet kokią, net ir labai sudėtingą schemą.
Laidžių nuoseklaus prijungimo problema
Būklė. Dvi lempos ir rezistorius yra sujungti grandinėje vienas už kito. Bendra įtampa yra 110 V, o srovė - 12 A. Kokia yra rezistoriaus vertė, jei kiekviena lempa yra 40 V?
Sprendimas. Kadangi svarstomas nuoseklus ryšys, žinomos jo dėsnių formulės. Jums tereikia juos teisingai pritaikyti. Pradėkite išsiaiškindami įtampos vertę rezistoriuje. Norėdami tai padaryti, iš bendros lemputės įtampą reikia atimti du kartus. Pasirodo, 30 V.
Dabar, kai žinomi du dydžiai U ir I (antrasis iš jų pateiktas sąlygoje, nes bendra srovė lygi kiekvieno serijinio vartotojo srovei), rezistoriaus varžą galime apskaičiuoti naudodami Omo dėsnis. Pasirodo, 2,5 omo.
Atsakymas. Rezistoriaus varža yra 2,5 omo.
Užduotislygiagrečių ir serijinių kondensatorių prijungimui
Būklė. Yra trys kondensatoriai, kurių talpa yra 20, 25 ir 30 mikrofaradų. Nustatykite jų bendrą talpą, kai jie prijungti nuosekliai ir lygiagrečiai.
Sprendimas. Lengviau pradėti nuo lygiagretaus ryšio. Esant tokiai situacijai, tereikia pridėti visas tris reikšmes. Taigi bendra talpa yra 75uF.
Skaičiavimai bus šiek tiek sudėtingesni, kai šie kondensatoriai bus sujungti nuosekliai. Galų gale, pirmiausia reikia rasti vienybės santykį su kiekviena iš šių pajėgumų, o tada pridėti juos vieną prie kito. Pasirodo, vienetas, padalytas iš bendros talpos, yra 37/300. Tada norima vertė yra maždaug 8 mikrofaradai.
Atsakymas. Bendra nuoseklaus prijungimo talpa yra 8 uF, lygiagrečiai - 75 uF.






