Omo dėsnis yra pagrindinis elektros grandinių dėsnis. Kartu tai leidžia paaiškinti daugelį gamtos reiškinių. Pavyzdžiui, galima suprasti, kodėl elektra „nemuša“ant laidų sėdinčių paukščių. Fizikai Ohmo dėsnis yra labai svarbus. Be jo žinios būtų neįmanoma sukurti stabilių elektros grandinių arba visai nebūtų elektronikos.
Priklausomybė I=I(U) ir jos reikšmė
Medžiagų atsparumo atradimo istorija yra tiesiogiai susijusi su srovės įtampos charakteristika. Kas tai yra? Paimkime grandinę su nuolatine elektros srove ir apsvarstykime bet kurį iš jos elementų: lempą, dujų vamzdį, metalinį laidininką, elektrolito kolbą ir kt.
Keisdami atitinkamam elementui tiekiamą įtampą U (dažnai vadinamą V), stebėsime per jį einančios srovės (I) stiprumo pokytį. Dėl to gausime formos I \u003d I (U) priklausomybę, kuri vadinama "elemento įtampos charakteristika" ir yra tiesioginis jo rodiklis.elektrinės savybės.
V/A charakteristika skirtingiems elementams gali atrodyti kitaip. Paprasčiausia jo forma gaunama įvertinus metalinį laidininką, kurį padarė Georgas Ohmas (1789-1854).
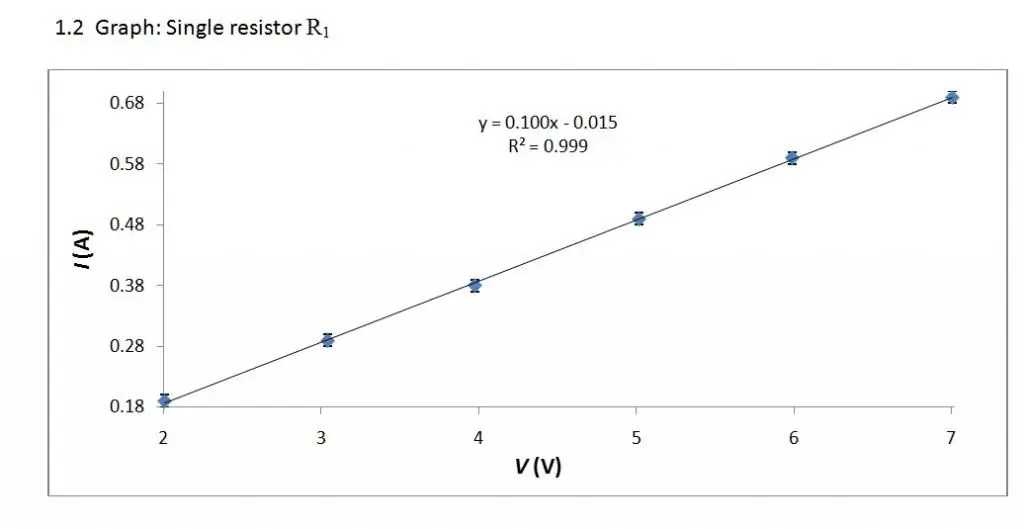
Voltų amperų charakteristika yra tiesinis ryšys. Todėl jo grafikas yra tiesi.
Įstatymas paprasčiausia forma
Ohm atliktas laidų srovės įtampos charakteristikų tyrimas parodė, kad srovės stipris metalinio laidininko viduje yra proporcingas potencialų skirtumui jo galuose (I ~ U) ir atvirkščiai proporcingas tam tikram koeficientui, tai yra I. ~ 1/R. Šis koeficientas tapo žinomas kaip „laidininko varža“, o elektrinės varžos matavimo vienetas buvo Ohm arba V/A.
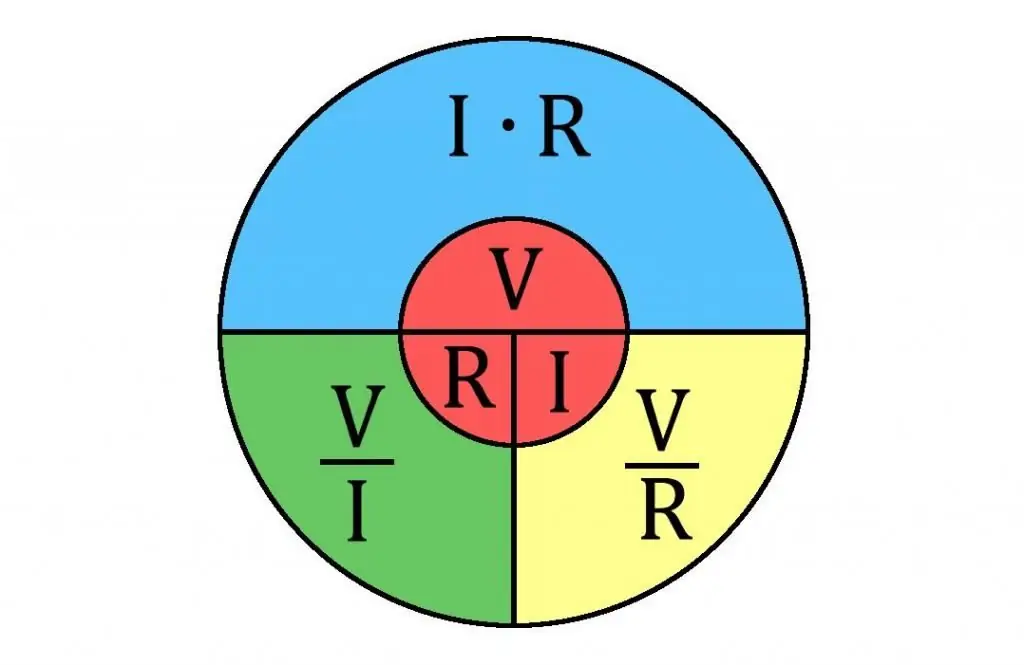
Dar vienas dalykas, į kurį reikia atkreipti dėmesį. Omo dėsnis dažnai naudojamas skaičiuojant varžą grandinėse.
Teisės formuluotė
Omo dėsnis sako, kad vienos grandinės sekcijos srovės stipris (I) yra proporcingas šios atkarpos įtampai ir atvirkščiai proporcingas jos varžai.
Pažymėtina, kad tokia forma dėsnis galioja tik vienalytei grandinės atkarpai. Homogeniška yra ta elektros grandinės dalis, kurioje nėra srovės š altinio. Kaip naudoti Ohmo dėsnį nehomogeninėje grandinėje, bus aptarta toliau.
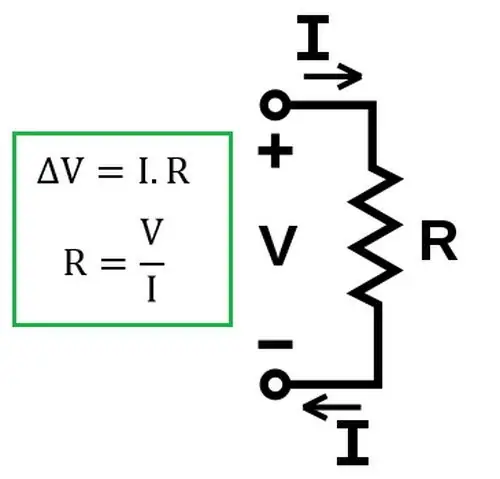
Vėliau eksperimentiškai buvo nustatyta, kad sprendimams įstatymas lieka galiotielektrolitai elektros grandinėje.
Fizinė pasipriešinimo reikšmė
Atsparumas yra medžiagų, medžiagų arba terpės savybė, neleidžianti pratekėti elektros srovei. Kiekybiškai 1 omo varža reiškia, kad laidininko, kurio galuose yra 1 V įtampa, gali praeiti 1 A elektros srovė.
Elektrinė savitoji varža
Eksperimentu buvo nustatyta, kad laidininko elektros srovės varža priklauso nuo jos matmenų: ilgio, pločio, aukščio. Taip pat nuo jo formos (rutulio, cilindro) ir medžiagos, iš kurios jis pagamintas. Taigi, pavyzdžiui, vienalyčio cilindrinio laidininko varžos formulė bus tokia: R \u003d pl / S.
Jei į šią formulę įdėsime s=1 m2 ir l=1 m, tai R skaitine prasme bus lygus p. Iš čia apskaičiuojamas laidininko varžos koeficiento SI matavimo vienetas - tai Ohmm.

Savosios varžos formulėje p yra varžos koeficientas, nustatomas pagal medžiagos, iš kurios pagamintas laidininkas, chemines savybes.
Norėdami apsvarstyti diferencinę Ohmo dėsnio formą, turime apsvarstyti dar keletą sąvokų.
Srovės tankis
Kaip žinote, elektros srovė yra griežtai nustatytas bet kokių įkrautų dalelių judėjimas. Pavyzdžiui, metaluose srovės nešikliai yra elektronai, o laidžiose dujose - jonai.
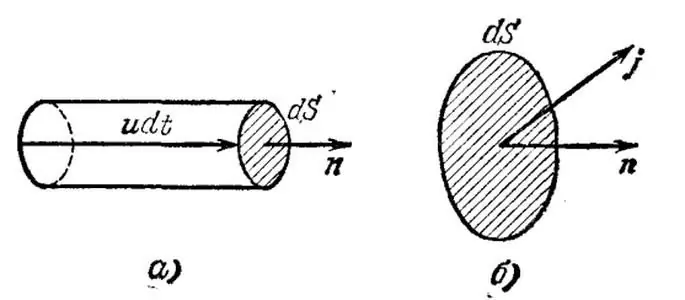
Paimkite trivialų atvejį, kai visi esami operatoriaivienalytis - metalinis laidininkas. Mintimis išskirkime be galo mažą šio laidininko tūrį ir u pažymime vidutinį (dreifą, sutvarkytą) elektronų greitį duotame tūryje. Be to, tegul n žymi srovės nešiklių koncentraciją tūrio vienete.
Dabar nubraižykime be galo mažą plotą dS, statmeną vektoriui u, ir pagal greitį sukonstruokime be galo mažą cilindrą, kurio aukštis udt, kur dt žymi laiką, per kurį praeis visi esamame tūryje esantys srovės greičio nešikliai. per sritį dS.
Šiuo atveju krūvis, lygus q=neudSdt, bus perkeltas elektronais per sritį, kur e yra elektrono krūvis. Taigi elektros srovės tankis yra vektorius j=neu, nurodantis krūvio, perduodamo per laiko vienetą per ploto vienetą, kiekį.
Vienas iš Omo dėsnio diferencialo apibrėžimo pranašumų yra tai, kad dažnai galite išsiversti neapskaičiavę pasipriešinimo.
Elektros įkrova. Elektrinio lauko stiprumas
Lauko stiprumas kartu su elektros krūviu yra pagrindinis elektros teorijos parametras. Tuo pačiu metu kiekybinę jų idėją galima gauti iš paprastų eksperimentų, kuriuos gali atlikti moksleiviai.
Paprastumo dėlei apsvarstysime elektrostatinį lauką. Tai elektrinis laukas, kuris laikui bėgant nekinta. Tokį lauką gali sukurti stacionarūs elektros krūviai.
Be to, mūsų tikslams reikalingas bandomasis mokestis. Savo pajėgumu naudosime įkrautą korpusą - tokį mažą, kad jis nepajėgus sukeltibet kokie trikdžiai (krūvių perskirstymas) aplinkiniuose objektuose.
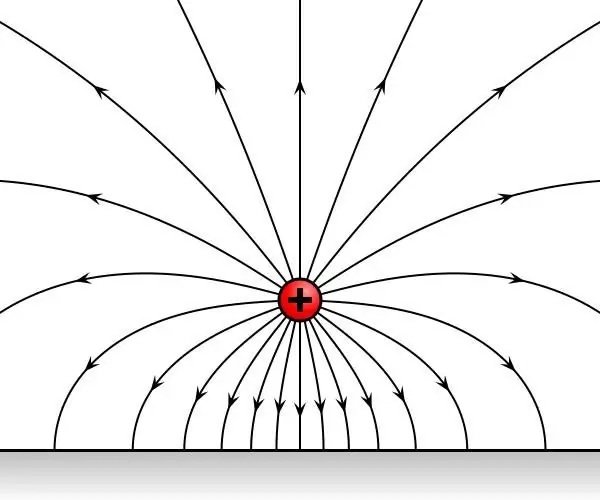
Paeiliui panagrinėkime du bandomuosius įkrovimus, paeiliui išdėstytus viename erdvės taške, kuris yra veikiamas elektrostatinio lauko. Pasirodo, kad k altinimai bus paveikti nekintamo laiko įtaka iš jo pusės. Tegul F1 ir F2 yra jėgos, veikiančios krūvius.
Apibendrinus eksperimentinius duomenis, buvo nustatyta, kad jėgos F1 ir F2 yra nukreiptos arba į vieną, arba į priešingomis kryptimis, o jų santykis F1/F2 nepriklauso nuo erdvės taško, kuriame pakaitomis buvo išdėstyti bandomieji krūviai. Todėl santykis F1/F2 yra pačių krūvių charakteristika ir nepriklauso nuo lauko.
Šio fakto atradimas leido apibūdinti kūnų elektrizaciją ir vėliau buvo vadinamas elektros krūviu. Taigi pagal apibrėžimą paaiškėja, kad q1/q2=F1/F 2 , kur q1 ir q2 - viename lauko taške pateiktų mokesčių suma, o F 1 ir F2 - jėgos, veikiančios krūvius iš lauko pusės.
Iš tokių svarstymų eksperimentiškai buvo nustatyti įvairių dalelių krūvių dydžiai. Sąlygiškai nustatę vieną iš bandomųjų įkrovų, lygių vienam, galite apskaičiuoti kito įkrovimo vertę išmatuodami santykį F1/F2.
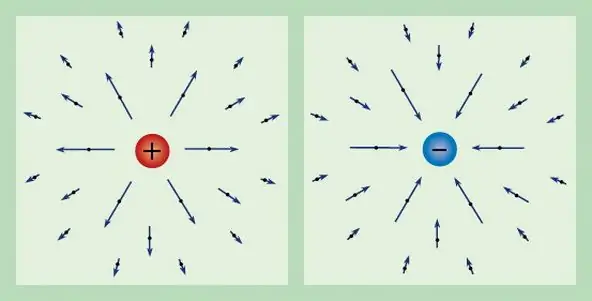
Bet kurį elektrinį lauką galima apibūdinti pagal žinomą krūvį. Taigi jėga, veikianti vienetinį bandomąjį krūvį ramybės būsenoje, vadinama elektrinio lauko stipriu ir žymima E. Iš krūvio apibrėžimo gauname, kad stiprumo vektorius turi tokią formą: E=F/q.
Vektorių j ir E jungtis. Kita Ohmo dėsnio forma
Vykstame laidininke įkrautų dalelių tvarkingas judėjimas vyks vektoriaus E kryptimi. Tai reiškia, kad vektoriai j ir E bus nukreipti kartu. Kaip ir nustatant srovės tankį, laidininke pasirenkame be galo mažą cilindrinį tūrį. Tada per šio cilindro skerspjūvį praeis srovė, lygi jdS, o į cilindrą tiekiama įtampa bus lygi Edl. Taip pat žinoma cilindro savitosios varžos formulė.
Tada dviem būdais surašę srovės stiprio formulę, gauname: j=E/p, kur reikšmė 1/p vadinama elektriniu laidumu ir yra atvirkštinė elektrinei varžai. Paprastai jis žymimas σ (sigma) arba λ (lambda). Laidumo vienetas yra Sm/m, kur Sm yra Siemensas. Vienetas atvirkštinis omui.
Taigi, galime atsakyti į aukščiau pateiktą klausimą apie Ohmo dėsnį nehomogeninei grandinei. Šiuo atveju srovės nešiklius veiks elektrostatinio lauko jėga, kuriai būdingas intensyvumas E1, ir kitos jėgos, veikiančios juos iš kito srovės š altinio, kuris gali būti pažymėtas E 2. Tada buvo taikomas Omo įstatymasnehomogeniška grandinės dalis atrodys taip: j=λ(E1 + E2).
Daugiau apie laidumą ir varžą
Laidžio gebėjimą pravesti elektros srovę apibūdina jo savitoji varža, kurią galima rasti pagal varžos formulę arba laidumą, apskaičiuojamą kaip laidumo atvirkštinę vertę. Šių parametrų reikšmę lemia tiek laidininko medžiagos cheminės savybės, tiek išorinės sąlygos. Visų pirma, aplinkos temperatūra.
Daugumos metalų savitoji varža normalioje temperatūroje yra jai proporcinga, tai yra p ~ T. Tačiau nukrypimai pastebimi esant žemai temperatūrai. Daugeliui metalų ir lydinių, kurių temperatūra yra artima 0 °K, varžos skaičiavimas parodė nulines vertes. Šis reiškinys vadinamas superlaidumu. Pavyzdžiui, tokią savybę turi gyvsidabris, alavas, švinas, aliuminis ir tt Kiekvienas metalas turi savo kritinę temperatūrą Tk, kuriai esant stebimas superlaidumo reiškinys.
Taip pat atkreipkite dėmesį, kad cilindro varžos apibrėžimas gali būti apibendrintas laidams, pagamintiems iš tos pačios medžiagos. Šiuo atveju skerspjūvio plotas iš varžos formulės bus lygus laido skerspjūviui, o l - jo ilgiui.






