Mokant fiziką 10 klasėje, svarstoma dipolių tema. Ką reiškia ši sąvoka ir kokios formulės naudojamos jai apskaičiuoti?
Įvadas
Jei įdėsite dipolį į vienodo elektrinio lauko erdvę, galite jį pavaizduoti kaip jėgos linijas. Dipolis yra sistema, kurioje yra du identiški parametrai, tačiau jie yra priešingi taškiniai krūviai. Be to, atstumas tarp jų bus daug mažesnis nei atstumas iki bet kurio dipolio lauko taško. Dipolio momento samprata nagrinėjama elektrodinamikos mokykliniame kurse (10 klasė).
Dipolio ašis yra tiesi linija, kertanti abiejų krūvių taškus. Dipolio ranka yra vektorius, jungiantis krūvį ir tuo pačiu pereinantis iš neigiamo krūvio dalelių į teigiamai įkrautas daleles. Elektriniam dipoliui būdinga tokia būsena kaip dipolis arba elektrinis momentas.
Pagal apibrėžimą, dipolio momentas yra vektorius, kuris skaitine prasme yra lygus dipolio krūvio ir jo peties sandaugai. Be to, jis nukreiptas kartu su dipolio petimi. Esant nulinei jėgų sumos lygybei, apskaičiuojame momento reikšmę. Kampui, esančiam tarp dipolio momento irelektrinio lauko kryptingumas, būdingas mechaninio momento buvimas.
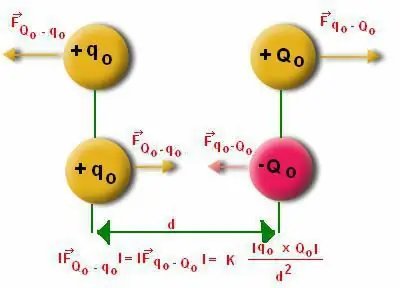
Dažnai žmonėms sunku apskaičiuoti modulį, veikiantį dipolio struktūrą. Čia būtina atsižvelgti į kampo "Alfa" skaičiavimo ypatumus. Yra žinoma, kad dipolis nukrypsta nuo subalansuotos padėties. Tačiau pats dipolio momentas turi atkuriamąjį pobūdį, nes jis linkęs judėti.
Skaičiavimai
Kai šis dipolio momentas yra nehomogeniško elektrinio lauko terpėje, neišvengiamai atsiranda jėga. Tokioje aplinkoje jėgų sumos rodikliai nebus lygūs nuliui. Vadinasi, yra jėgos, veikiančios taškinį dipolio momentą. Dipolio peties dydis yra daug mažesnis.
Formulę galima parašyti taip: F=q (E2 - E1)=qdE, kur d yra elektrinio lauko skirtumas.
Ieškokite tiriamos fizinės koncepcijos savybių
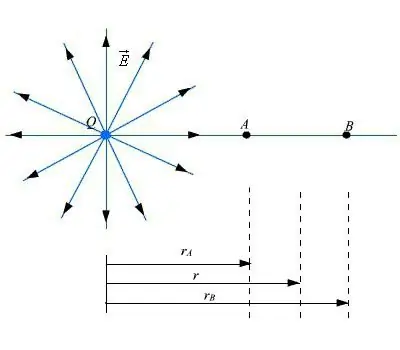
Pažvelkime į temą toliau. Norint nustatyti, kokia yra elektrinio lauko charakteristika, jei jis sukurtas naudojant krūvių sistemą ir lokalizuotas mažoje erdvėje, reikia atlikti daugybę skaičiavimų. Pavyzdžiui, atomai ir molekulės, kurių sudėtyje yra elektriškai įkrautų branduolių ir elektronų.
Jei reikia ieškoti lauko didesniu atstumu nei matmenys, sudarantys plotą, kuriame yra dalelės, naudosime keletą tikslių formulių, kurios yra labai sudėtingos. Galima naudoti ir paprastesnįapytikslės išraiškos. Tarkime, kad kuriant elektrinį lauką dalyvauja taškinių krūvių rinkiniai qk. Jie yra nedidelėje erdvėje.
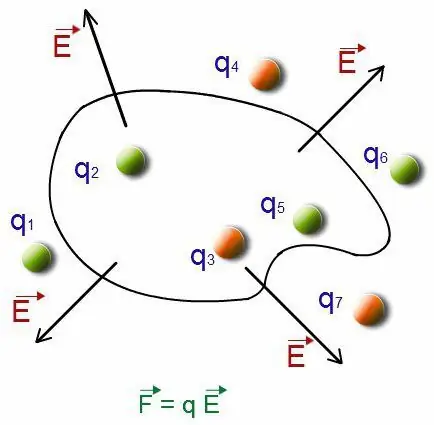
Norint atlikti lauko turimos charakteristikos skaičiavimą, leidžiama sujungti visus sistemos įkrovimus. Tokia sistema laikoma taškiniu krūviu Q. Dydžio rodikliai bus krūvių, buvusių pradinėje sistemoje, suma.
Mokesčių vieta
Įsivaizduokime, kad krūvio vieta yra nurodyta bet kurioje vietoje, kur yra mokesčių sistema qk. Keičiant vietą, jei ji turi ribas, išreikštas mažame plote, tokia įtaka bus nereikšminga, beveik nepastebima laukui žiūrint. Tokiose elektrinio lauko stiprumo ir potencialo apytikslėse ribose nustatymai atliekami naudojant tradicines formules.
Kai viso sistemos įkrovimo suma lygi nuliui, nurodytos aproksimacijos parametrai atrodys apytiksliai. Tai leidžia daryti išvadą, kad elektrinio lauko tiesiog nėra. Jei reikia gauti tikslesnį aproksimaciją, mintyse surinkite atskiras nagrinėjamos sistemos teigiamų ir neigiamų krūvių grupes.
Jei jų „centrai“pasislenka kitų atžvilgiu, lauko parametrus tokioje sistemoje galima apibūdinti kaip lauką, turintį du taškinius krūvius, vienodo dydžio ir priešingo ženklo. Pastebima, kad jie yra išstumti kitų atžvilgiu. PateiktiNorint tiksliau apibūdinti krūvių sistemą pagal šio aproksimavimo parametrus, reikės ištirti dipolio elektriniame lauke savybes.
Termino įvedimas
Grįžkime prie apibrėžimo. Elektrinis dipolis yra sistemos, turinčios du taškinius krūvius, apibrėžimas. Jie turi tą patį dydį ir priešingus ženklus. Be to, tokie ženklai yra nedideliu atstumu nuo kitų ženklų.
Galite apskaičiuoti dipolio pagalba sukuriamo proceso charakteristiką, kurią vaizduoja du taškiniai krūviai: +q ir −q, ir jie yra nutolę nuo kitų.

Skaičiavimų seka
Pradėkime apskaičiuodami potencialą ir intensyvumą, kurį dipolis turi savo ašiniame paviršiuje. Tai tiesi linija, einanti tarp dviejų įkrovimų. Su sąlyga, kad taškas A yra atstumu, kuris lygus r centrinės dipolio dalies atžvilgiu, ir jei jis yra r >> a, pagal lauko potencialo superpozicijos principą šiame taške bus racionalu naudokite išraišką elektrinio dipolio parametrams apskaičiuoti.
Stiprumo vektoriaus dydis apskaičiuojamas superpozicijos principu. Lauko stiprumui apskaičiuoti naudojama potencialo ir lauko stiprumo santykio sąvoka:
Ex=−Δφ /Δx.
Tokiomis sąlygomis intensyvumo vektoriaus kryptis nurodoma išilgai dipolio ašies atžvilgiu. Jo moduliui apskaičiuoti taikoma standartinė formulė.
Svarbupaaiškinimai
Reikėtų atsižvelgti į tai, kad elektrinis dipolio laukas susilpnėja greičiau nei jis patiria taškinį krūvį. Dipolio lauko potencialo mažėjimas yra atvirkščiai proporcingas atstumo kvadratui, o lauko stiprumas yra atvirkščiai proporcingas atstumo kubui.
Taikant panašius, bet sudėtingesnius metodus, dipolio potencialo ir lauko stiprio parametrai randami savavališkuose taškuose, kurių padėties parametrai nustatomi naudojant tokį skaičiavimo metodą kaip polinės koordinatės: atstumas iki elektrinio dipolio centras (r) ir kampas (θ).
Skaičiavimas naudojant įtempimo vektorių
Intensyvumo vektoriaus E sąvoka yra padalinta į du taškus:
- Radialinis (Er), kuris nukreiptas išilgine kryptimi tiesios linijos atžvilgiu.
- Tokia tiesė jungia nurodytą tašką ir dipolio centrą su statmenu jam Eθ.
Šis kiekvieno komponento išskaidymas nukreipiamas išilgai pokyčio, kuris vyksta su visomis stebimo taško koordinatėmis. Jį galite rasti pagal santykį, susiejantį lauko stiprumo rodiklius su galimais pakeitimais.
Ieškant vektoriaus komponentą ties lauko stiprumu, svarbu nustatyti galimų pokyčių, atsirandančių dėl stebėjimo taško poslinkio vektorių kryptimi, ryšio pobūdį.
Apskaičiuokite statmeną komponentą
Kai baigtaAtliekant šią procedūrą, svarbu atsižvelgti į tai, kad dydžio išraiška esant nedideliam statmenam poslinkiui bus nustatyta pakeitus kampą: Δl=rΔθ. Šios lauko dedamosios dydžio parametrai bus lygūs.
Gavus santykį, galima nustatyti elektrinio dipolio lauką savavališkame taške, kad būtų sukurtas vaizdas su šio lauko jėgos linijomis.
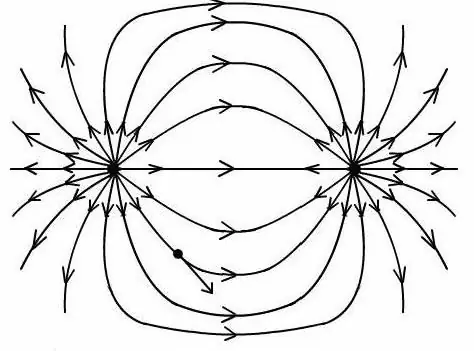
Svarbu atsižvelgti į tai, kad visos dipolio potencialo ir lauko stiprio nustatymo formulės veikia tik vieno dipolio krūvio verčių ir atstumo tarp jų sandauga.
Dipolio momentas
Aprašomo darbo pavadinimas yra pilnas elektrinių savybių aprašymas. Jis turi pavadinimą „dipolio sistemos momentas“.
Apibrėžiant dipolį, kuris yra taškinių krūvių sistema, galima nustatyti, kad jam būdinga ašinė simetrija, kai ašis yra tiesi linija, einanti per kelis krūvius.
Norėdami nustatyti visą dipolio charakteristiką, nurodykite ašies orientacijos kryptį. Kad būtų lengviau atlikti skaičiavimus, galima nurodyti dipolio momento vektorių. Jo dydžio reikšmė lygi dipolio momento dydžiui, o krypties vektorius skiriasi jo ir dipolio ašies sutapimu. Taigi, p=qa, jei a yra vektoriaus, jungiančio neigiamus ir teigiamus dipolio krūvius, kryptis.
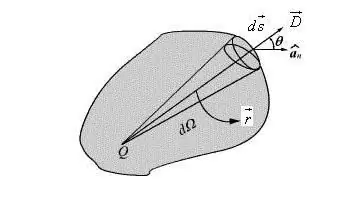
Naudoti tokią dipolio charakteristiką yra patogu ir daugeliu atvejų galima supaprastinti formulę ir suteikti jai formąvektorius. Dipolio lauko potencialo aprašymas savavališkos krypties taške parašytas vektoriaus forma.
Tokių sąvokų, kaip dipolio charakteristikos vektorius ir jo dipolio momentas, įvedimas gali būti atliktas naudojant supaprastintą modelį - taškinį krūvį vienodame lauke, apimantį krūvių sistemą, kurios geometriniai matmenys atitinka į jį nereikia atsižvelgti, bet svarbu žinoti dipolio momentą. Tai būtina sąlyga norint atlikti skaičiavimus.
Kaip elgiasi dipolis
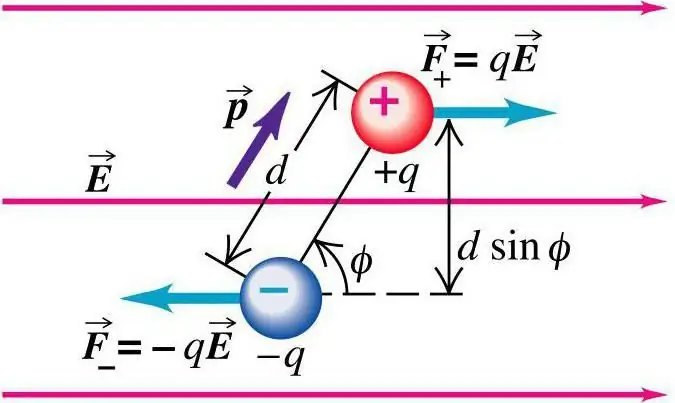
Dipolio elgesį galima pamatyti tokios situacijos pavyzdžiu. Dviejų taškinių krūvių padėtis turi fiksuotą atstumo pobūdį vienas kito atžvilgiu. Jie buvo patalpinti vienodo elektrinio lauko dipolio sąlygomis. Padarė pastabas apie procesą. Fizikos (elektrodinamikos) pamokose ši sąvoka nagrinėjama išsamiai. Nuo lauko iki užtaiso atliekami jėgų veiksmai:
F=±qE
Jų dydis yra vienodas, o kryptis priešinga. Bendros jėgos, veikiančios dipolį, rodiklis yra lygus nuliui. Kadangi tokia jėga veikia įvairius taškus, bendras momentas bus:
M=Fa sin a=qEa sin a=pE sin a
kur α yra kampas, jungiantis lauko stiprumo vektorius ir dipolio momento vektorius. Dėl jėgos momento sistemos dipolio momentas linkęs grįžti į elektrinio lauko stiprumo vektoriaus kryptis.
Elektrinis dipolis yra sąvoka, kurią svarbu aiškiai suprasti. Daugiau apie tai galite pasiskaityti internete. Taip pat galimokytis fizikos pamokose mokykloje 10 klasėje, kaip jau kalbėjome aukščiau.






